Einstein Hat Awards (entries 292-270)
Thank you to our sponsors, XTX Markets, UK Maths Trust, National Museum of Mathematics (MoMath.org), Amplify, G-Research, Jane Street and Dexter and Deborah Senft.
Contributors - Geoff Smith, Simon Coyle, Samuel Monnier, Dianne Flatt, Cindy Lawrence, Chaim Goodman-Strauss, Guillermo Acevedo, Kit Reagan, Hayley Richardson, Philipp Legner, Craig Kaplan, Robert Fathauer, Yoshiaki Araki, Dexter Senft, David Smith and Ewart Shaw.
292 Samuel Circle 16 USA
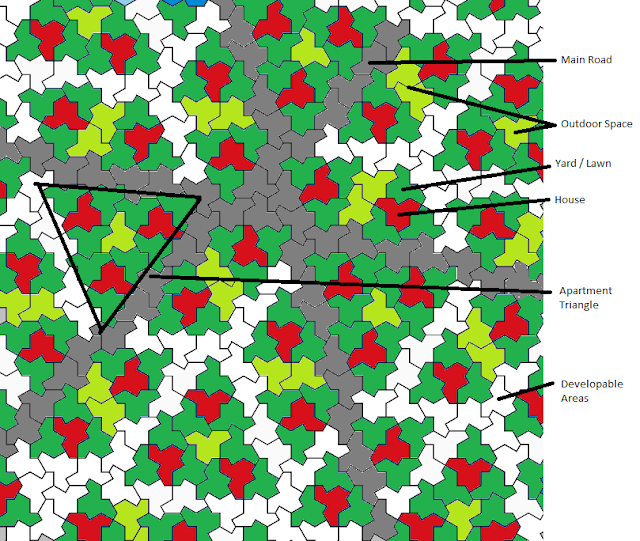
My idea is a new neighbourhood design, based on the relatively infrequent flipped monotiles. These tiles represent the houses, while the surrounding three tiles are the outdoor property of that house. When three of these sets of three form a triangle, this "block" becomes a set of apartments, and the tile they surround is a courtyard. House tiles that are not part of apartment blocks are connected by green space to another. Long stretches of uncategorized tiles are set as main roads for easy transportation. The benefit of this design is that the structure is not monotonous, in fact it never repeats. Another positive attribute is the incorporation of natural areas within the design in an organic manner.
291 Pedro Azevedo 15 Brazil
"The idea behind this picture is to combine the concept of the Einstein tile with the iconic figure of Albert Einstein, playing on the shared name to convey a more profound message that can't be noticed when the picture is not analysed thoroughly. The hat that was put on Einstein's head was handmade and later edited through editing apps and it also aims to play around with another name that can be attributed to this interesting shape: the Hat Tile. Moreover, it symbolizes the timeless connection between people's creativity and mathematical exploration. This juxtaposition suggests that although the Einstein tile was recently discovered, the idea it represents – the boundless potential within our minds – has always existed. This picture may also reinforce that profound discoveries are not only found in the external world but are waiting to be unlocked within our own imagination. The hat that was placed on Einstein's head emphasises the significance of creativity and individual expression in the process of discovery
This idea demonstrates the famous origami magic trick, Fold-N-Cut. Being an origami artist, I utilized my love for paper folding to illustrate the fascinating Einstein Monotile! I initially wanted to make this for MOVES 2023 but didn't get a chance to. I'm so glad to have my idea come to fruition on this wonderful occasion!
289 Julianna Calabia 16 USA
Drawing from the suggestion of fiber arts, I chose to crochet my Einstein Mad Hat tessellation. I enjoy crocheting, and a cool thing about the craft is that it can only be done by hand. There are knitting machines, but due to the three-dimensional aspect of crocheting, the closest machines can do is mimic the look of crochet, not actually replicate it.
My design for the Einstein Mad Hat was based on a crochet hexagon granny square. I then folded the hexagon into thirds and sewed up the seams in order to create the look of a section of the tile. To create the full tile, I repeated this process for a total of four individual hexagon thirds and then connected those pieces together to make an Einstein Mad Hat tile.
In the images, the colorful Einstein Mad Hat tiles are the final (and larger) version, while the blue/green crocheting was my mock-up to test my design idea. I tried several strategies before deciding on this one, as it worked the best to achieve my goal.
In a unique fusion of technology and creativity, I harnessed the power of an AI generator called "Perchance" to craft a mesmerizing visual experience. With a set of carefully curated prompts, this AI created chiral aperiodic polygons that harmoniously tessellate the canvas, but with an intriguing twist – they do so without ever repeating themselves. The result of this artistic endeavour is a symphony of shapes and patterns, intricately woven into the serene canvas of a coffee latte and the vibrant world of fiber arts. As you immerse yourself in these creations, you'll find a balance between the familiar and the utterly unique, a testament to the boundless potential of human-AI collaboration. From the comforting warmth of your coffee latte to the delicate craftsmanship of fiber arts, these chiral aperiodic wonders invite you to explore the infinite possibilities of art, technology, and the imagination.
287 Anna Paulino 17 USA
With trial and error, the development and correction of the pattern took a little over 3 hours, with each tile being about 20 minutes afterwards; ((9 white tiles + 1 yellow tile) x 20 minutes) totalling to about 7 hours dedicated towards the making of this brilliant and vibrant hat. Although not very visible, each of the white pieces on the top are shaped like individual hat tiles, including the main yellow one in the middle, truly encompassing the beautiful partnership between fiber arts and mathematics in the fall season!
286 Daniel Weiner USA
Humans ‘invent’ a new shape in the same way Sir Isaac Newton ‘invented’ gravity. An aperiodic monotile was always there. My submission titled The Einstein Bulb imagines how, just as being unaware of gravity didn’t stop us from taking in the majesty of the moon rising in the night sky, the hat could exist in nature just waiting to be discovered and explored. Please see image one for the piece itself and image two for a peek into the process.
285 Willian Fry 12 USA
MONTRIS
The project I have made combines the hat tiles with the game Tetris. It works very similarly to the game Tetris, but instead there are aperiodic monotile hat tiles. You can move the tile using the arrow buttons and you also can flip the tile. You can do so by pressing the space key. You can turn the tile by pressing the up or down key. The up key turns the tile clockwise, and the down key turns the tile counter-clockwise. When you get a whole row, that rows shift down. You try preventing the tiles from getting to the top of the screen. There is roughly 25% chance of need to have a flipped tile available, according to the pattern.
The discovery of the Einstein's tile, or the Hat Spectre, has generated a lot of interest and intrigued others to learn more about its practical uses. I decided to use UNO cards for my project since it's a logical, mathematical, and educational game in addition to being entertaining. Like mathematicians who experiment with different forms, lengths, angles and numbers of sides in an attempt to find that one special, aperiodic solution from a single shape, UNO requires the player's knowledge and abilities. Moreover, just as David Smith endeavored to align shapes based on criterias, to find aperiodicity, UNO players must logically understand when to best fit each card into the game by matching their colours, numbers, or even functions. Furthermore, the following shape that was named as "hat" can be also seen as an analogy to the magic trick in which the rabbit appears from the magician's top hat in magic shows, conveying the aspect of surprise, which can also be seen in UNO as you will never expect your opponents next move.
283 Leslie Fry 14 USA
The Einstein hat tiles remind me of dear old Paddington bear's hat. And we all know that:
"A wise bear always keeps a marmalade sandwich in his hat in case of emergency." In this case, he will have plenty of marmalade sandwiches, won't he?
I created this image by cutting real whole wheat and white bread with raspberry and marmalade jam into hat shapes. I photographed and rearranged the hats according to part of the aperiodic tessellation using photoshop. Hope you find it delicious...and sticky!
282 Shirley McDonald 69 USA
This reversible hat is made with mathematics fabric in the shape of the aperiodic monotile. The two images show both the inside design and outside design of the hat. The quilted hat includes cotton batting which helps it hold its shape. I plan to wear this hat to the next local mathematics teacher meeting. With the choice of a light or dark hat, it should match with most any outfit.
281 Emily McDonald 31 USA
My Hat and Spectre Tiles creation is a necklace and earrings set that shows one string of the aperiodic monotiles that never quite repeat the pattern. Before creating these two pieces, I searched online to ensure there is not already jewelry available inspired by the Hat and Spectre tiles. I was not able to find any jewelry from a Google search or on Etsy that use or reference Hat and Spectre tiles. The earrings and necklace are made with thin plywood and gold wire. This necklace and earrings set is one of a kind just like the aperiodic monotile!
280 Brian Trease 46 USA
No sketch, no pencil, no ruler, no protractor? No problem! No grid, no compass, no phone, not even the internet?? Still no problem at all!
Prepare to summon your inner mathemagician and behold the way of the Fold-and-Cut method for polygon generation. ONE SINGLE CUT is all it takes to free our elusive geometry from a folded sheet. Armed with only a square sheet of paper and a pair of scissors, follow my example to directly conjure your own Einstein Hat Monotile, anytime, anywhere!
MAGIC
Over twenty years ago, mathematicians proved the Fold-and-Cut Theorem … that ANY polygon can be generated by a “single straight complete cut” across a properly folded pattern. (See https://en.wikipedia.org/wiki/Fold-and-cut_theorem). For the Hat Monotile, this new rendition not only invites mere static admiration, but launches dynamic participation in its very genesis. One bold snip becomes a sacred act of creation, marking the transformation of an ordinary piece of paper into a mathematically exact Einstein tile ready for tessellation. Further, the universal appeal of origami nicely complements the rich mathematics of monotiling. Combining the phenomenon of Einstein tiling with hands-on geometric paper-folding (along with a dash of magical flair!) greatly multiplies the capacity for outreach, education, and inspiration.
FOLDING
For completeness, a depiction of the fold-lines on a square sheet is included in the submitted photos, with mountain folds in red and valley folds in blue. While the pattern itself is an artifact of intrigue, the true beauty is that an aspiring geometrician doesn’t even need it to make the necessary folds. In fact, I have sequenced a folding algorithm that requires no initial markings at all.
Only seven actual folding operations are prescribed, which one can perform in nearly the same time it takes to fold an origami crane. Another dozen folds are made along the way to establish useful crease lines. The final folded form, which I’ve dubbed the “tulip”, is compact and ready to be snipped, with a visible crease marking the cutting line. In all, it takes only six minutes to fold and then another half second to execute the defining cut.
PERFORM
Envision yourself in a classroom or at a party, ready to dazzle your audience. With the same flourish of pulling a rabbit out of a hat, you create mesmerizing geometry with one dramatic snip. Perhaps you have pocketed a stash of pre-folded “tulips” ready to produce as needed. The “tulip” is a wonderful prop, as it can be easily opened to show its initial square shape, then quickly collapsed back to its folded state in seconds. You might even pull them out of an actual hat before executing the cut! Or perhaps there is time to complete all the folds from scratch, with the unsuspecting audience joining along to create their own “tulips”, crease by crease.
CATERING? YES!
While the spectacle of single-cut Hat Tile generation is more than enough to entertain myself for hours, I am happy to illustrate its novel application to broader fields, such as the catering arts.
Imagine … you receive a gala invitation that includes a mysterious pre-folded “tulip”, with no explanation and only instructions to bring it along. Upon seating at the event, the wait staff produces a pair of shining silver scissors. Holding your tulip high in the air for effect, they snip it in half with a flourish, scraps dropping to the table. You are handed back your tulip and unfold it to discover you now hold an Einstein Hat Tile! Perhaps you are next directed by words written on it, to incorporate it into a master tiling at the head table. And perhaps one-side-colored paper is used, and perhaps you are even among the lucky one-out-of-every-seven to receive a reversed tile, with the color on the backside.
For more informal settings, instead imagine simply receiving square placemats or menus, preprinted with the pattern of mountain and valley folds on the backside. Perhaps the guests are simply allowed to experiment and take them home. Or, perhaps instructions are given to fold the paper, after which the hosts demonstrate the method of the single cut. After everyone admires their own creations in awe, all are invited to pin them to the event’s message/best-wishes board, personally extending the never-repeating tessellation.
And lastly, indulge yourself by imagining the perplexed bemusement of an entire audience of unsuspecting mathematicians (all well-versed in the geometry, hype, and style of the Einstein tile) upon following the same actions described above, unfolding their freshly cut pattern, and discovering the fruits of such geometric trickery at play in their hands.
MULTIPLY
An often unstated yet essential quality of the canonical origami crane is its ability to be generated almost anywhere by anyone. We aspire to likewise perpetuate the enchantment of the Einstein Hat. By sharing this newfound fold-and-cut power of creation with others, may the monotiles multiply and forever tessellate the infinite plane.
279 Ally Stanley 28 UK
Unlike similar, tetromino-based games that lower from the top, the tiles are positioned anywhere on the board and then locked into place. You can clear rows in 4 different ways: "straight" rows and "hexagonal" rows in two diagonal directions each (some of these are highlighted in the second image). A row is cleared by completely filling it. The board above then falls down to fill the gap, creating new space at the top. Once you can no longer place hats, the game is over.
It may be tempting to come up with a deterministic "system" to beat the game, but the random appearances of reflected tiles - about 12.7% of the time, of course - put a stop to that. Museum guests might wonder if it's possible to play indefinitely. I hope that it would encourage them to keep thinking about the game at home and explore more of the wonderful world of aperiodic tiling.
278 Aravah Chaiken 16 USA
Einstein Mad Hatter Tea Party Gingerbread Cookies with Royal Icing (the Proof is In the Pudding).
In terms of process, I began by printing out paper tiles and playing around with tessellating them. While putting together the paper tiles in order to see what my final design would look like, I found that the ratio was the same as the ratio that I had researched: about one reflected cookie was needed for every seven regular cookies. I could not flip the cookies over after baking and had to cut two reflected ones in advance because the gingerbread domed in the oven and the cookies could not be turned upside down. Despite cutting the cookies before baking, I had to cut them again after baking while they were soft because they had spread enough that they no longer had the angled edges necessary for the tiles to fit together. I would appreciate if MoMath would sell a hat cookie cutter because hand cutting the cookies was time-consuming.
In order to apply the four color theorem, I picked four colors that would complement the tessellation design and each other. In order to ensure that I applied the four color theorem correctly, I marked each cookie with its color before icing them to ensure that the four color theorem was satisfied. To answer your final question, my family ate them. And they were delicious!
277 Corinne Kirkpatrick 18 USA
For this competition, I was heavily inspired by not only the connective nature of the Hat and Spectre tiles but also the name of the tiles specifically the word hat. To represent the connective nature of the Hat and Spectre tiles I decided to make my submission entirely out of folded Post-it notes. Specifically, the way the Post-it notes are slotted together and maintain their shape represents how when the Hat and Spectre tiles are put together there exists no overlap or gaps between the tiles. While the Post-its don't make a true tessellation, I did make sure that there were different folding methods in each part of the submission. After deciding on the materials for this submission, I was left with the problem of what to make, looking at the name of the tile, the idea came to me, a hat. It was critical for me to have my creation functional. All of this led me to make my submission, a hat completely made of Post-it notes representing Hat and Spectre titles that is not only geometric but wearable!
276 Abe McCann 13 USA
I wanted to make a chainmail version of the shape, but unfortunately could not gain access to a 3D printer. I know that hurts my chances, but figured I'd submit anyway. Thanks!
275 Isaiah Mogerman 13 USA
A mobius strip made out of Hats.
274 Sy Chen 61 USA
Ever since I read the news of the hat shape discovery, I have been thinking about an origami version of the einstein hat. After several failed attempts with a modular approach using either a four-unit diamond shape or an eight-unit kite shape, I started to work on a single-piece version. Finally, I came up with the one-piece solution published in the OrigamiUSA website, https://origamiusa.org/thefold/article/diagrams einstein-hat-mathematical-puzzle.
I came up with a revised version late June this year. This new version shows 4 connected twin-kite pentagons on one side using folded edges. Each hat was folded from a piece of square without cutting. Photo 1 is one of the tiling examples. Photo 2 shows the assembled tiles from the dollar bill units designed in July this year, each folded from a $1.00 bill without cutting. It took me roughly 8 mins to fold a dollar bill hat and 9 mins for a hat from a square.
273 Iroha Uda 15 USA
A hat where the rim and the top are the hat and spectre tiles. The first file includes photos of me making it as proof that I was the one making it, the second file has the completed product.
272 Guilherme Cavalcanti 15 Brazil
Displayed on a canvas measuring 70cm x 60cm, the Fibonacci Sequence Tile captures squares arranged in accordance with the Fibonacci sequence, the painting features tiles measuring 1cm, 2cm, 3cm, 5cm, 8cm and 13cm in size. Each square, with its distinct dimensions, aligns to create a pattern, representing the infinite sequence where each number is the sum of the two preceding ones.
271 Sophie Cheng 16 USA
270 Ally Stanley 28 UK
"C of Turtles"
A periodic tiling of a hyperbolic surface based on the molecular structure of diamond (chemical formula "C").
Inspired by Gerard Westendorp's "Einsteinhedra" and Jon-Paul Wheatley's "Hat Trick" balls, this piece takes advantage of a twisting effect on einsteinhedra by varying their base tile on the Tile(a, b) continuum.
The second image illustrates this effect. The hat tile results in tetrahedral, octahedral, and icosahedral einsteinhedra with holes that align exactly with the faces of their dual polyhedra: a twist of 0°. The spectre and turtle tiles give einsteinhedra with holes that are twisted by different amounts. In fact, the turtle tile twist (new dance move?) is such that connected einsteinhedra are twisted by almost exactly half their angle of rotational symmetry. For the tetrahedral case the twist is 55.59154...° (instead of 60). The tile that gives a perfect 60° twist is Tile(1, b) where b = (3-sqrt(3))/2 = 0.63397... very close to the turtle but not exactly equal. This tile gives the twist needed to construct a diamond cubic structure from tetrahedral einsteinhedra.
Side note: Tile(1, b) gives icosahedral units whose opposite pentagonal holes align perfectly. This allows us to build a rhombic triacontahedron with only 32 units versus the 92 required (regular) dodecahedra by linking the vertices directly. My rendition of a "turtlecontahedron" is also available on request (although I don't think it looks as nice).