Einstein Hat Awards (entries 97-73)

Thank you to our sponsors, XTX Markets, UK Maths Trust, National Museum of Mathematics (MoMath.org), Amplify, G-Research, Jane Street and Dexter and Deborah Senft.

Contributors - Geoff Smith, Simon Coyle, Samuel Monnier, Dianne Flatt, Cindy Lawrence, Chaim Goodman-Strauss, Guillermo Acevedo, Kit Reagan, Hayley Richardson, Philipp Legner, Craig Kaplan, Robert Fathauer, Yoshiaki Araki, Dexter Senft, David Smith and Ewart Shaw.

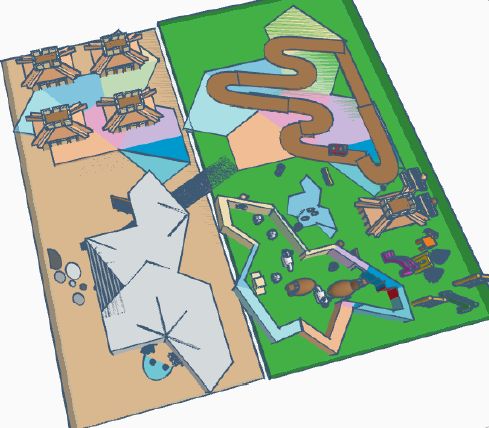
97 Rhia Raj 11 UK

https://www.tinkercad.com/things/3RXAnhtRZOQ?sharecode=V2flJ-F9ctT4Fihr5ScbAwG0gQpR_rTYW5V8TgN-osA

A link to the aperiodic monotile. Rhia has created a small village/town using the Einstein tile in as many different ways as possible! The model should be viewed in 3D hence the link above - please contact r.legg@parmiters.herts.sch.uk if the link does not work.

96 Rosie Neville 16 UK

For my creation, I wanted to both showcase the beauty and creativity that maths can take the form of- whether that be in a practical or artistic way. Hence, I decided to use the item of a clock- one of the most globally used and quitencential items used by hundreds to showcase the brilliance of the aperiodic monotile. Being a long term fanatic of maths and the UKMT maths challenges one of the most striking elements of this tile to me was its composing metatiles used in the proofs- of which I found most amusing the similarity between the hexagonal metatile and the UKMT logo. This led to me deciding that I would use this metatile as the primary outline for the clock, while employing the colours composing of the UKMT, as an honourable acknowledgment of the key part that UKMT has played in my love for maths and deeper exploration into non-typical 'school maths'.

To futher embed the unique traits of the 'hat monotile' within my design, I decided to construct the timings of the clock using only the ratios of the side dimensions of the tile: namely 1 and root 3.

Though definitely a challenge to construct the clock and placing the tile tessellations accurately (despite its misleading seeming simplicity!), I greatly enjoyed the challenge and hope that many more challenges encompassing the creativity and real life applications and demonstrations of mathematic structures arise in the future! Only time will tell ...

95 Aiden Wong 13 UK

The Einstein Room

I decided to submit this handmade ‘Einstein Room’, as I call it, is because my entire family were designers, and design various things from Disney tin box in the 90s to clothings, and also because it uses the Einstein tile creatively, from carpet to painting on the wall. I also made it in only white paper is to show the symbolism of how simple but sophisticated the Einstein tile is. 1 tile can tile up an infinite plane but it took years and years to discover. In this 3D Artwork, I made a TV with the tile behind for aesthetics. An Einstein tile carpet, a sofa with its cushions made up of two Einstein tiles that fit if you put them together, an Einstein tile clock, a painting with the tile inside, a coffee table and shelfs to make the room less empty.

94 Sarah Poiani 26 USA

This quilt is inspired by the einstein tile discovered last year. Each tile was divided into its 8 component kites to make it more feasible to sew. It is quilted with the spectre tile overlaying each einstein tile to show that the spectre, unlike the einstein, does not need to be reflected to tile the plane. The border is an arrangement of trapezoids (referred to by quilters as half-hexies) and demonstrates a periodic tiling.

93 John Nephew 53 USA

As a game publisher and creative maker, I'm intrigued by the potential applications of the "hat" aperiodic monotile, especially with its relationship to the hexagon that's popular as an element in tabletop game design. To properly explore its potential, I need to be able to make a lot of hats! So I've made laser-cut aluminum molds to produce hats with a benchtop injection molder, using recycled plastic that's been shredded with Precious Plastic open-source machinery. This is faster than 3D FDM printing, and the result is a much more satisfying object to hold because it's solid plastic.

The next step is to build an industrial mold for producing recycled plastic tiles in larger quantities, with greater precision, and using and diverse colors and materials. I'm working with an experienced mold designer to do this, and will be running a Kickstarter from October 17th through November 16th to fund the tooling costs (information at atlas-games.com/infunity).

By themselves, the hats are an intriguing open-ended puzzle. The real value in the injection molding is to enable mass production of affordable recycled plastic tiles, to unlock more creative experiments at a larger scale, from game design to furniture making to interior decoration.

92 Mason Bassett 35 USA

I'm a classically trained timber framer and have always enjoyed taking on challenging projects. I graduated from the American College of the Building Arts with a major in Timber Framing in 2013 and have been honing my craft ever since. I've always sought out projects that push the boundaries of what is geometrically and physically possible. This may include figuring complex geometrical shapes such as how does an ogee dormer intersect with an onion dome or how do I clear span 40+ feet to create a grand hall of a wedding venue.

When I came across the Einstein Tile, my first thought was how do I build a timber framed outdoor classroom with this shape? The real challenge here was to think outside the periodic building box. Most timber frames are very repetitive and by design periodic but this would require something very different.

I started with a Einstein tiled roof surface but aesthetically it needed more texture. Therefore, I raised three of the tiles above the main roof and sloped them in different directions. Next, I needed an equally impressive support structure for such an unique roof line. I experimented with a variety of post configurations but none set well with me. I eventually settled on this suspended roof concept. Using 2 parabolas in a quasi-tensegrity structure I suspended the roof over a concrete pad that also is is tiled in the Einstein Tiles. The resulting outdoor classroom is a one of kind piece that combines several different mathematical concepts into unified design.

Although this is rendering at the moment there is very little stopping me from building it for a museum or university somewhere. I'll need to work with an engineer to finalize timber sizes and cable placements but what I have (based on my experience) is close to what the final product could look like. The other great thing about this design is that it can be scaled up and down to accommodate most situations. The tile size or the number of tiles could be changed with little effort.

Thank you for putting together this competition. It's been a real joy on my part to design this entry and learning more about math along the way.

91 Jonas Wittke 46 USA

Hello! To celebrate the discovery of the hat monotile (not to mention the infinite family of spectre monotiles!) I have created an approachable, Sudoku-style puzzle called "Hat Sudoku".

The puzzle can be accessed here: https://tinyurl.com/yu2hp5zq

Rather than a standard 9x9 square sudoku grid, this puzzle uses the same segmented hexagonal grid upon which the hat monotile is formed. Therefore, the "hats" in this puzzle are true to form! Further, the seven hats together can be recognized as the "H-7 Supertile," which is used to make larger and larger patterns of monotiles.

This is far from the first "variant" Sudoku puzzle, but it is almost certainly the first and only variant Sudoku employing monotiles and segmented hexagons. I will "eat my hat" ... ahem ... "eat my aperiodic monotile" if I am proven wrong about this.

"Approachable" is a hotly-contested term among Sudoku constructors and solvers alike... to the degree that an entire Discord server is devoted to "Genuinely Approachable Sudoku". This puzzle submission is, genuinely (!), approachable and is suitable for all ages and all levels of expertise. There are numerous entry points to solving the puzzle, but there is only one correct solution.

Congratulations to David Smith and his collaborators for their incredible discovery, and congratulations in advance to You, Hat Sudoku Solver!

90 Geoff Ginader 49 USA

Congratulations to the discoverers of the amazing aperiodic monotile!

I am pleased to present my entry for The Einstein Mad Hat Competition!

I created a unique costume for our local "comic con" conference, brick, and cosplay event.

The event was Comicon-Erie held September 9, 2023 at the Erie Bayfront Convention Center, Erie, PA, USA.

With this costume, I got the opportunity to become one of these elusive mathematical wonders.

The costume was developed with precision cut papers imported to a home digital paper cutter using .svg files created from CAD software. The basic shape is a kite exactly 1/6 of a hexagon. The monotile was assembled from eight such kites into the famous einstein hat shape, and then rolled to the t-shirt to make the costume. The mirror image of the tile is the back of the costume in all-black so that the mirror tiles would look different when assembled.

I thought at the conference I would receive many high fives from smart people who had heard the news. As it happened, the only person I met that week who already knew the story of the Hat was a college math professor who did chuckle at the costume idea.

I suppose the einstein is best appreciated when fit together with hundreds of mates. Alas, my t-shirt remained a true monotile that day. Unfazed, I know I have Halloween this month when I hope to find dozens of tiles just my size and dressed-to-fill.

89 Pheobe Hart 12 UK

I decided to make a 3D printed box and print each individual hat and stick them on individually. This whole printing process took a few weeks. We also 3D printed a box. I then sat down and sanded each piece by hand with a nail file and then I worked out how the pattern Tessellates (this is different on each side) this whole sticking process took about 6 hours. Once they were all stuck down I coated them in primer and let that dry then put on the first coat of orange paint over the whole box using the air gun. I then let that dry over night and on the next day I used special tape to stick over the hats I wasn’t painting over and then cut out the shapes of where we were going to paint. The next colour we were applying was dark blue. Once that had all dried we then had to paint the black on the rest of the hats. After the painting process which took about 1 and a half hours it was time to go in to the final stages where we did a final coat in a protective layer and attached all the edges to tidy up the corners.

88 Isabella Smith 12 UK

I chose this design because it is a unique creation whilst also being practical. I have made it patchwork to symbolise the shapes inside of the original pattern . It can be worn over the head or just on the shoulder so it is practical for all ages and all heights . As a result of the original shape this bag could potentially be infinitely expandable.

87 Shameer Ali 16 UK

Hello! My name is Shameer Ali and I'm thrilled to introduce my latest project, an engaging puzzle that will put your problem-solving skills to the test. Here's a comprehensive overview of what you can expect:

This puzzle journey begins with the fascinating world of steganography. Your initial task is to employ steganography tools to unveil a concealed link tucked away within an image (Start.jpg). Following this link will lead you to another image (TheHat.jpg), which contains a mathematical operation to solve. But that's just the tip of the iceberg.

When you open this mathematical image as text, you'll uncover an encrypted line in base64 nestled at the very bottom. Decipher this line to reveal four additional digits. Add these digits to the solution of the mathematical problem, and you'll be rewarded with an ISBN to a book titled "The Odd 1s Out." The title of this book serves as a clever hint for the next phase of your puzzle adventure.

Within the image, opened as text after the encrypted line, you'll discover 26 coordinates, each accompanied by a string of 3-2 characters. Considering the book's title, you can deduce that the coordinates and strings located in odd positions should be disregarded.

But that's not all. Enter these coordinates into a map, and you'll unlock the shape of the hat tile, with the exception of one enigmatic special coordinate.

(The shape is an approximation to avoid any pattern within the coordinates and so making the finding of the not related coordinate easier and without the need of plotting the coordinates in a map)

The intrigue deepens as you combine all the characters next to the even-positioned coordinates. This will yield a link that demands deciphering via a Caesar cipher. The outcome of this decryption will furnish you with a YouTube link.

Now, in the YouTube video, you'll encounter an audio message in Morse code. When decoded, it will instruct you to "Add to the answer '.rf.gf'."

Here's the delightful twist: add '.rf.gf' to the special coordinate, and it will transport you to a website titled "The Hat Tile Secret." Gain entry by inputting the password, which is "Einstein." Inside this site, you'll discover a page housing a video titled "The Hat Tile Secret" – the thrilling culmination of this intricate puzzle.

But here's the kicker: the video contains a classic Rick Roll, a song famously used as a meme and for pure amusement. This was the puzzle's ultimate purpose - to reveal the lighthearted use of the Hat Tile. In my case, I've imbued it with the role of being a source of entertainment.

Prepare to embark on an adventure filled with codes, clues, and a good dose of humor. Are you up for the challenge? Best of luck!

Warm regards,

Shameer Ali

Skills used for this project:

1. Steganography

2. Cryptography

3. Mathematics

4. Image Editing

5. Web Development

6. Mapping

7. Problem-Solving

8. Creative Writing

9. Morse Code

10. Video Editing

11. Attention to Detail

12. Sense of Humor

13. Testing and Quality Assurance

14. Storytelling

15. Project Management

16. User Experience Design

17. Online Hosting

18. Research

86 Johannes Martin 47 Germany

Wang tile like decomposition of the hat tile clusters into hexagon shapes. It's fun. There are 18 hexagons in total in 6 states of rotation.

85 Debbie Swartzel 57 US

This is a quilted wall hanging of the Hat shape. My son sent me the New York Times article and suggested this be my next English Paper Piecing project.

English Paper Piecing is a hand pieced quilting technique where each individual shape-in this case the kite- is basted onto a paper foundation that provides the stability needed to to sew pieces together. This technique allows for sharper angles than what can usually be achieved on a domestic sewing machine. I made about 80 Hats then sewed them together before appliquéing the resulting piece to the background fabric.

The quilt top was then loaded on a longarm sewing machine specifically designed for quilting (see second photo) and quilted with straight line quilting so the quilting would not overpower the Hats.

While I used one of the diagrams as my inspiration, I needed to use more than four colors since I would not have the ability to have each Hat outlined. Each Hat had to stand on its own and same color Hats could not have adjacent sides touching without losing the shape.I chose a palette of 7 colors for the main Hats and a white for the mirror image Hats.

My daughter is a math instructor at Appalachian State University and the quilt will hang in her office.

84 Starr Shumaker 49 US

These are 2 drawings I drew in the last month utilizing the Einstein Hat as inspiration.

83 Bowen Ping 21 China

First image: it shows the combinatoric equivalence between regular hexagon, hat tiles, H7/H8 clusters and their super-tiles. There are ten classes of tiles according to their joint, colored differently.

Second image: hat tiling can be convert to equivalent regular hexagon tiling, so it is possible to obtain hexagonal Wang tiles and tiling according to the hat hexagon tiling. The super-tile structure is shown as green cluster with a red pentagram in the center, separated by deep-purple tree-like part.

82 Isabelle Campbell-Smyth 11 UK

I have chosen this design because of its title and meaning. I simply turned the top of the hat into the actual shape. This Piece may look like a graduation hat, I made it like this to symbolise intelligence and accomplishment link to its name. The little book I suggested, was just to say a little bit about it and how the title was formed.

80 Emily Kelt 17 UK

Sales pitch: "Introducing the Einstein Hat Tile Drinking Glass – where mathematical precision meets artistic flair! This uniquely designed glass is more than just something to drink from; it's a fusion of mathematics and design.

Picture this: your favourite beverage in a glass that captivates your mind. The smooth, geometric sides of the Einstein Hat Tile Drinking Glass are a result of the careful balance between mathematical precision and aesthetic appeal. It's not just a glass; it's a conversation starter, a reflection of your appreciation for the beauty found in both mathematics and art.

Elevate your drinking experience with a touch of genius – because why settle for ordinary when you can sip from a glass that's both calculated and captivating? "

I designed and modelled a drinking glass that's shape is exactly the same as the Einstein Hat Tile using Fusion 360 (a CAD program). I created a poster to advertise it (and the sales pitch above). I have been fascinated by tiling patterns and geometry since I was young; I distinctly remember sitting on a sofa and looking at the tessellation pattern on the carpet. The drinking glass would certainly be very different from the typical glasses! The problem I have found in my house is that the cupboard storing our drinking glasses is overflowing, and so I designed a solution! As a unique repeating shape, the Hat could be rearranged so that many glasses would fit in the cupboard. The edges are smooth and the corners slightly rounded so that it is ergonomic. (the shape of the Hat also looks like it would be fun to hold! As a climber I can see the many places to hold it and drink from it). The second image is a mock-up of what the design would look like if it was used as a vase for a tulip - another funky application of this shape.

79 Isabelle McAloon 11 UK

This is an arty shape featuring all of the subjects at my school. I love to participate in every class every day and I hope you like my shape. It is a tessellect puzzle putting little and big pieces of the hat together.

78 Lars Eriksson 56 Sweden

The first picture shows the design made from the Spectre tile. In my own research I focus on modular tiling, mostly on 5-fold pattern. The basis is the polygon in contact method by Hankin. I've used the same approach on the Spectre tile. To get a more organic look I've let the crossing lines bloom out into curved lines in the motif of the tile.

The second picture shows the underlying grid of the Spectre tiles (with some ornamental motif for me to learn about the dynamics of how the tiles provide visual opportunities.

The pattern contain two unfilled areas. They are the result of an insight I got when playing around with the Spectre tiles, ending up with two ways of rotating it, getting two symmetric areas (which can't be tiled with the Spectre tile). I filled them with some text.

Of course these "holes" isn't necessary and for the core idea of tiling the plain they fail the task. I'm sure the pattern can be tiled without them with minor changes. I didn't want to be constraint by the established tiling approach many early adopters have been using. The downside is that I can't tell if the way I started out tiling this pattern (without the "holes" can be tiled indefinitely from a pure mathematical point of view.

77 Ryder Izbrecht 15 UK

Eventually, barcodes and QR codes will run out, therefore a replacement is needed. A possible replacement is a HAT code that uses the aperiodic monotile created by David Smith, Joseph Myers, Craig Kaplan and Chaim Goodman-Strauss. Due to the tile never repeating its shape an infinite amount of codes will be available, eradicating the problem of its exhaustion. Similarly to QR codes the HAT code would have to be in black and white or monochromatic colours to have an easily identifiable and scannable code, the only problem would be for companies being unable to have customisable codes to match their firm and marketing.

76 Lukas Kavaliauskas 11 UK

This is my beautiful art

75 Bradley Klee 36 USA

The art of rewriting all the definitions in not just one, but two different ways that both seem to contradict arbitrary aesthetic choices of the original article:

https://resources.wolframcloud.com/FunctionRepository/resources/HatTrialityTree/

https://resources.wolframcloud.com/FunctionRepository/resources/HatHexagons/

74 Jon-Paul Wheatley 36 US

A ball constructed from 12 pentagons and 60 hat tiles. The color of the panels was pulled from the original paper about the hat.

Here's a 60s video documenting the ball being made: https://www.instagram.com/p/Cx5KzMnuNYv/

73 Arley Walker 13 UK

To show my love for the hat and its wonderful aperiodic monotile properties I have created a patchwork wall hanging.

I created the wall hanging using the historical quilting method called English Paper Piecing (EPP for short), which was developed in 1770.

This involves cutting out each shape from card (I split each hat up into 4 separate equal jewel-like shapes, each jewel is the same as combining two kites).

Then, I cut a piece of fabric to wrap around the paper piece. Which I secured using a needle and thread with a stitch on each corner.

When wrapped, you can again use a needle and thread to join them together to get the hat by following the pattern I created.

Repeating this numerous times I made multiple hats, which I then combined to make a patchwork.

When I had made the pattern it was time to turn it into a wall hanging, I added batting (stuffing) and a large piece of backing fabric.

I used the sewing machine to combine it all together and add the lines dividing each hat into 8 kites. This shows how the hat is composed, as well as keeping the front, batting, and back together.

Finally, I added the binding (fabric around the edge to neaten the edge). I also completed this on the sewing machine.

I did all this without any prior experience. Previously, I didn't even know how to thread a needle let alone combine over 80 Jewel shapes!

Thankfully, my mum is extremely experienced with sewing. After seeing her impressive patchworks, I knew I had to combine my maths nerdiness with my creative side to produce something similar.

I wanted to complete this completely by myself, so she taught me a skill - such as wrapping a shape - and I would then go off and do it until I was confident with that ability then she would teach me another.

I estimate that I spent 50 hours on this patchwork, spending an average of 2 hours a day on creating this wall hanging for about 25 days. It measures 67 cm tall and 63 cm wide and is made up of about 90 individual pieces.

Because I practised each skill many times I now know how to fully make a quilt and could make another one if I wanted to. And maybe I will, I really enjoyed making this and it is really rewarding to see it hanging above my bed and thinking, 'I made that!'