Einstein Hat Awards (entries 214-188)
Thank you to our sponsors, XTX Markets, UK Maths Trust, National Museum of Mathematics (MoMath.org), Amplify, G-Research, Jane Street and Dexter and Deborah Senft.
Contributors - Geoff Smith, Simon Coyle, Samuel Monnier, Dianne Flatt, Cindy Lawrence, Chaim Goodman-Strauss, Guillermo Acevedo, Kit Reagan, Hayley Richardson, Philipp Legner, Craig Kaplan, Robert Fathauer, Yoshiaki Araki, Dexter Senft, David Smith and Ewart Shaw.
214 Łukasz Wojtas 38 Poland
213 Michelle Tsai 27 USA
My submission is a hand-knit sweater vest featuring the Hat Tile. I wanted to combine my love of mathematics with my love of knitting, and found that making a hat tile knitting pattern was the perfect blend of the two! The Hat Tile sweater vest, which I named "Hattie" for reasons that should be apparent, is knit flat, bottom-up, and uses a predominantly intarsia-based technique for the colorwork. The ribbed borders for the arm holes and neckline are knit in the round.
I did every step of the process myself, from conceptualizing the design, drafting the pattern, selecting the yarn colors and texture, and, of course, knitting the vest. It turns out it's quite difficult and time-consuming to create a knitting "pattern" of an aperiodic monotile where the whole point is that there is no repeating pattern! I'm thrilled with the results, and am excited to get to add a little more math into my daily wardrobe. I hope that when I wear my hat tile vest to class, it can inspire more conversations with my math students about exciting new discoveries in the field :)
212 Maria Graff 41 Norway
One jacket with the spectre tile as quilted pattern.
Up cycling three dresses and four tops, this textile art is a fully functional jacket ready for the chilly autumn days.
The exterior is making a texture between three different patterns, the smallest one is of the brocade in one of the garments, then comes a subtle chessboard pattern formed by the black and semi black and finally sewn together with a unison Spectre pattern for the three layered fabric of the quilt.
This is my first quilt I have ever made. As I am a landscape architect, the distribution of patterns over a surface area and creation of beauty isn’t new for me.
Feel free to tag me if you post the image on social media: Maia_T_Graff
211 Kirby Currie 16 UK
I chose to make a set of 8 different coloured, magnetic Einstein hat tiles. These magnetic hats would be suitable for a classroom setting to give learners an interactive hands on experience to develop understanding of the hats’ properties an spark interest. The hats could be used in classrooms in a range of ways: games/recreation, decoration, and teaching.
As they are magnetic, they can be used on classroom whiteboards or ''mini-whiteboards'' (which most schools in the UK use and are mainly compatible with magnets) as well as any flat surface.
I chose to make my tiles in 8 different bright and bold colours, to be eye catching and engaging for children and to make it easy to differentiate between the coloured pieces as my hats have an extra layer of challenge: tile the hats so no sides of tiles the same colour are touching.
I counted and I could not find more than 6 different tiles touching another, so the minimum amount colours was 6 + the root tile making 7, but I added an extra because the pattern never repeats meaning there could potentially be a chance of 7 tiles sharing with 1 tile, so I chose 8 colours.
This adds and extra layer to the concept but also, I feel, highlights the beauty of the tiling, making it an attractive product that could be used outside of a just a classroom setting and in places like, on the fridge for children in the home to play with, a mathematicians fridge or just for anyone who find the colours and patterns (though technically speaking there is only one) appealing and wants them for aesthetic purposes or a fun game for when they are bored in the kitchen.
I find them fascinating to tile and during the making process, did spend a while playing around with their tiling as it is not as simple as meets the eye, as of course there isn't a repeating pattern.
To make them I used adhesive magnetic sheets and coloured adhesive vinyl-which is very hard wearing, I tessellated the maximum number of tiles for the size I wanted on the magnetic sheets using a single paper cut-out template and pencil, to reduce waste and make the process more efficient, after this I hand cut out my 32 pieces, making sure to do it as accurately as possible to ensure the hats would fit together.
I made an equal number of the mirror image hat and of those I made an equal number in each colour, this is because my assumption was that over a larger area there would be a 50:50 distribution of the mirrored tiles and equal amount of colours to make it fair.
I then cut out the vinyl and stuck and adhered them to the hats.
Then I had a go tessellating them on my fridge and I let my younger sister have a go to check it was user friendly, she too found it a fun challenge.
As explained above, this is a prototype of a product which is a fusion of gameplay, art, maths, and education- or G.A.M.E. for short !
210 Jonas Lannoo 30 Belgium
Hi! I'm Jonas, a maker and mathematics enthusiast! The last years I am triggered by aperiodic tilings (such as the 15 types with pentagons) and was amazed by the discovery of the hat and spectre monotiles! My passion is to investigate and convert interesting mathematical principles to something special and visually attractive using electronics. Therefore I designed and created the electronics, hardware and software for a modular LED display using hat-"pixels".
The system exists out of two different modules, H7 and H8 clusters, as described on page 18 (fig 2.11) from the "an aperiodic monotile" paper. This allows to fill the plane indefinitely using only these modules and thus create a display of any shape and size. Each hat in the clusters exist out of of 4 LEDs. De display has a total of 748 LEDs, is driven by a small microcontroller (ESP32) and can show patterns, images, videos, gifs or streamed camera images over wifi. A custom script converts the images or frames to the exact pixel colours for the hat polygons (or the four sub-polygons per pixel per hat) and sends it's values over MQTT to the display.
209 Elliot Wilcox 45 UK
A small lap quilt, featuring the 'Einstein Hat' aperiodic monotile.
Assembled by sewing machine using the raw edge applique technique, then quilted by hand.
Blues were selected as a reflection of the first image of the tiles released, also a reflection of the fabric I had in my fabric pile.
208 Ridoy Mirdha Queen 16 UK
I have used the ''mad hat tile'' to produce a bookmark. The process of this was as follows : the material used was cardboard, I carefully traced the mad hat tile's shape using a printed copy of it onto the cardboard, I then made several copies of the tile and cut them apart. Then i joined them together using PVA glue on the sides, in a way that it would not have a repeating pattern. I folded some of the sides of the mad hat tile, this is a function of the bookmark where the flaps can be used to hold the pages. I had used a red and yellow paint and paintbrush and carefully painted the mad hat tiles. The bookmark's use is suitable for normal sized books.
207 Bronna Butler 73 US
This elegant 4.25" × 3.5" nightlight literally shines light on the aperiodic hat monotile. Amber stained glass was painted with vitreous paint and fired in a kiln, then wrapped in lead came and soldered to a nightlight fixture.
206 Tobias Hartley 13 UK
This picture shows elephants walking around on lovely green fields and lakes.
205 Theodore Hartley 11 UK
This is a picture of some colourful hat tiles, with some monochrome tiles interspersed.
204 Tom Edgar 43 USA
This cartoon depicts a Spectre wearing a Hat and riding a Turtle. The idea is that studying math is often a wild ride with many ups and downs. The discovery of these tiles represents a high amongst many years of lows (coming close to finding Einstein tiles but not being successful).
203 Lucy Birkinshaw 51 UK
Spectre/Hat and Turtle wallpaper installations.
Project overview:
My proposal is to make a series of hand-printed wallpaper installations featuring the new Einstein shapes, the ‘Spectre’, ‘Hat’ and ‘Turtle’. I would like to celebrate the collective effort that has been made to understand the properties of these new Einstein shapes by placing a series of similar, yet locally different paper designs in some of the institutions where individuals have worked on this.
The first Einstein shape cluster printed should obviously be presented to David Smith in Yorkshire, the person who started all this excitement.
Design inspiration:
I have been investigating the relationship between the ‘mostly Hats and a few Turtles’, and ‘mostly Turtles and a few Hats’ tilings that are equivalent to the Spectre tilings. I have been looking at how one layers over the other once they have been scaled to fit the same area. It is a dynamic ever shifting relationship. I have found a nice simple stripe adornment for the tiles that makes it easy to see how Turtles creep past Hats on the different layers as you travel from one Mystic to the next. The exact pattern of overlap between layers will be determined by the local density of ‘Mystics’.
Traditional hand-blocked wallpaper naturally produces a very welcoming and beautiful texture and suits this kind of project where placement of elements needs to be varied, and different layers can be built up.
I enjoy working with clients to produce bespoke colourways, block design and configurations that are site-specific. Designs could be very simple forms similar to those shown in the hand-drawn working sketches supplied, or much more elaborate. To my mind many of the design elements are like layers of lace. This is one style that could be explored. I would also like to make some versions with ‘flipped’ versions of the design relative to others to highlight the way the substitution rules in one of the proofs create a switch between the different ‘right’ and ‘left’ versions of the tiles.
Mathematical workings:
I have used a framework of regular hexagons to generate both the ‘Turtles surrounded by Hats’ and ‘Hats surrounded by Turtles’ tilings. I have used the proportion of ‘odds’ to ‘normals’ as 1: 4+√15. I have rotated the grid by 15 ° to get the best alignment. I’d really appreciate it if you could let me know if I have made a mistake here.
Thanks, and future collaborations:
I would like to take the chance to congratulate all those involved in these inspiring new discoveries. I would also like to thank those who have taken the time to present this work to the wider world either in podcasts, papers, or the fabulous ‘Hatfest’. It is wonderful for this new area of research to be accessible for all to join in.
The best place to see my previous and current work is on my Instagram account (see below).
I am always keen on collaborating in the field of Sciart and if you have any available wall space that could be covered in beautiful hand-printed bespoke wallpaper either now or in the future, then please get in touch.
The artist:
Lucy Birkinshaw specialises in designing, making, and installing bespoke block-printed artworks and has been making rooms full of wallpaper for over five years. She has a science background and has recently installed six walls of paper in collaboration with the University of Gloucestershire. They were created within time and budget and were funded by Arts Council England.
‘She has come up with some beautiful designs–they are complex and abstract, representing patterns, forces and processes which underpin the research undertaken by psychologists, social scientists, biologists, and geographers. …We thought they were wonderful.’
Dr Caroline Mills – Head of the school of Natural and Social Sciences (April 2022).
202 Tadeas Martinat 16 UK
My entry is in the form of an mp4 file so I'm sending it as a link to a Google drive file:
https://drive.google.com/file/d/1e9kXqK7nzucw_JlRFUWQTnjnSkzaZZnh/view?usp=sharing
How was this created?
The introduction is made using a software oscillator which was fed a wavelength in the shape of a hat, producing the audible sound as the rate the oscillator processes the shape at increases over time.
The melodies are programmed by tracing around hat / arrangements, for which I wrote an algorithm in Python that I fed a sequence of side lengths and side indexes representing each hat / arrangement. It then converted this sequence into midi files, mapping side index to pitch and side length to pitch duration. Each side of an individual hat tile is numbered 1 to 13, which, coincidentally, maps perfectly onto a full octave in the standard western 12-tone equal temperament. I chose to map the pitches onto one ascending 13th arpeggio of B minor and then a descending 13th arpeggio of C# minor. This also coincides with the 13 sides, however I do recognise the arbitrarity of key and harmony choice which weren't choices made based on any solid reasoning.
The rhythms were decided by the respective lengths of each mapped side, consisting of 1s, a 2 in each hat and square root 3s. These were then mapped onto the pitches as durations, usually in a 2:1 side length to beat ratio, however some variety is present such as the reflected hat (which represents the bass) is programmed using a 1:2 side length to beat ratio and chains are constructed using a 4:1 or even 6:1 ratio.
The final composition of MIDI files was created in a DAW where I assigned a different sound to each hat arrangement and added some miscellaneous effects.
The video was created as a visual guide to show which hat arrangements are 'playing'. I also added miscellaneous effects here, it obviously makes it much more interesting. As a small addition, the video is loopable.
Descriptions in order of appearance
reflected hat - across the aperiodic tiling, reflected hats are scattered throughout. This puts into question for some whether this really is a monotile aperiodic tiling due to the reflected shape being considered as a different shape, however mathematically the 'two shapes' are identical (congruent).
hat shell - around each reflected hat, there is a three-hat shell of unreflected hats. This also has another use for creating coordinate geometry of the tiling which will be mentioned later.
oriented chain - through each reflected hat passes an oriented chain of unreflected hats, which ends at its intersection with any other chain
reflected tile + tile - if two neighbouring reflected and unreflected tiles are merged into one, the hat tiling becomes a 1:1 mapping of a regular hexagonal tiling, which is an interesting observation and another link to the kite-divided hexagons which can be merged to initially form a hat shape.
metatile 1 - here is a return of of the three hat shell, which is the first instance of a 'metatile'. It represents a way which allows for simpler coordinate geometry mapping of the hat tiling by using the rough outlines of each
metatile, which can then be translated into its respective number and arrangement of hats.
metatile 2 - this is another metatile hat arrangement, which in reality represents two or three metatiles when taking into account their orientation or merging of three neighbouring metatiles where possible.
unreflected metatile hat - a singular unreflected tile is also a metatile, which is only present as its own object (not connected to any other metatile) when surrounded by other three triangular metatiles, however it is obviously more significant for it making up the vast majority of the tiling if taking into account reflected tiles as separate shapes.
Miscellaneous observations
The aperiodic nature of the tiling means that there is no clear time signature, as the music never repeats. This means that the only possible time signature is one which calculates the entire composition as one measure, making it, in this specific case, 235/8. For the same reason, extremely irregular polyrhythms are present.
Due to the irrational nature of square root 3, there is obviously no real note name to describe the rhythm it creates if used as a pitch duration. The closest possible approximation would be a double dotted crotchet, representing 1.75 beats, which is ~1.73205080757, however because I created the rhythms programmatically in this composition, they are accurate to 6 decimal places. The other two possible durations (1 or 2) can be easily described using real note names such as semiquavers, quavers, cortchets or minims, as they fit into all used side length to beat ratios.
201 Charlie Cao 14 UK
Using a colouring of a section of the tiling to create an image of Einstein (the second image demonstrates the process)
200 Rei Ishikawa 17 UK
A deconstructed cheese and ham toastie
199 Marianna Philips 32 USA
Abstract butterfly wings on an infinite blue sky, hand cut and painted with acrylic and ink on paper. Created by Marianna Phillips, artist instagram @WEIRDLITTLELINES
198 Fatma Kayatekin 25 Taiwan
Aperiodic tiling is a rebellious force in design since it reveals hidden beauty of asymmetry. The tessellation of the world map design draws inspiration from the profound concept of aperiodicity, which mirrors the essence of human individuality. Despite our shared humanity, our distinctiveness, born of our diverse cultures, colors, and languages, grants each of us a unique and precious quality. Just like how aperiodic tiling creates a captivating pattern regardless of repetition, people, like mono tiles, connect across the world through their unique qualities and differences. Each tile in the design is a symbolic representation of a human being, and the inspiration of the tile design lies in the metaphor of a precious gemstone: the diamond. Diamonds, renowned for their brilliance and singularity, symbolize the exceptional nature of each individual and the irreplaceable contributions they make to the world.
197 Jessica Jarvis 17 UK
football made from Einstein's hat, each tile hand cut and hand sewn together. In order to turn this unrepeatable shape into a pattern, I discovered I had to first start with a pentagon as a centre and attach five hats to its edges (I got this inspiration from a classic football), this gave me a larger pentagon shape which once met with more pentagons, was able to form a ball.
The discovery of the hat, turtle and spectre tiles is a remarkable advancement in mathematics with significant repercussions in architecture and engineering. Whilst Penrose tilings have long been used, this discovery takes it to a new level.
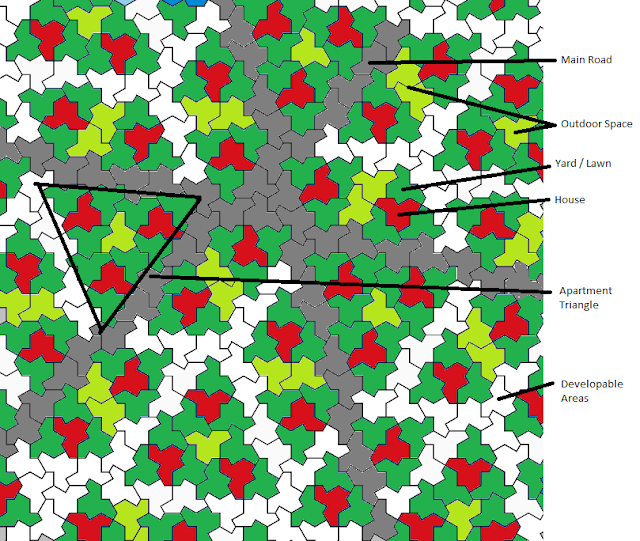
One of the key challenges within architecture and design is the achievement of modularity without the creation of uniform spaces. Thomas Heatherwick recently commented on the ‘blandemic’ in architecture, referring to the monotony of buildings in modern cities. However, it is impossible to ignore the productivity gains and financial savings associated with modular and repetitive buildings. Modular construction is viewed as the future of the industry as demand grows, but is often associated with dull and uninspiring designs. This new tiling is interesting as it can achieve both highly repetitive modularity and a fantastic space for people - a humanizing and intriguing design from simple building blocks.
The design presented is for a tensegrity shading canopy. It has one module that repeats on a grid of slender columns, allowing it to be manufactured off-site and installed quickly. However, walking underneath it leads to a sense of discovery, always finding somewhere different.
Each module consists of a tensegrity net which supports a taut fabric shading piece. The edge has a continuous ring beam and the scalloped edges of the fabric celebrate the repeated module. Such a shading device can be easily expanded or reconfigured if required. It is lightweight and when viewed in plan, celebrates the ideas of the underlying tiling. The level of customizability from a single module is incredibly exciting.
Overall, this canopy celebrates the discovery of the tiling by using simple shading modules to tessellate an outdoor space. It provides a beautiful, intriguing and ethereal space whilst leveraging the benefits of modularity.
195 Kerry Polzin 63 USA
Image 1 depicts the 'Tiger tile' which was created for use to introduce the Einstein hat tile to children. Image 2 is a collage board which shows multiple versions that were created in the development of the 'Tiger tile' as well as a couple of events where the 'Tiger Tile' Einstein hat was used to engage younger children as they were introduced to this latest discovery in mathematics.
194 Anita Yu 41 USA
I love this playful interpretation of the Hat which I transformed into a bubble wand. I feel the beauty of mathematics is something to be enjoyed by people of all ages and what better way to represent that than with bubbles. It is whimsical, colorful, and accessible to all no matter your level of math education. Even better, this Hat bubble wand was made from recycled plastic. The combination of the material and solution highlight the images reflected in each Hat showing how even the individual bubbles themselves create images that tessellate. This creation celebrates the Hat from different perspectives through multiple dimensions while having infinite hours of fun.
193 Tasnim Hossain 13 UK
Here is my submission for the Einstein Mad Hat Competition. As seen in the first picture I am wearing it as a sort of shawl. It was first invented to be a hijab but we realised it suited it as a shawl. I first intended to be used as a hijab because I am Muslim and wear it myself. I chose it to have many different colours because I love colour. I think, although it didn’t turn out to be what it was first intended for, it suits it much better as a shawl. It might be a bit useless or a bit useful I’m not sure but it was something I made. Something I had a lot of fun making it and in some ways I’m a bit upset it’s finally finished. But glad. I poked myself to many times to pin the shapes down. When I first saw the shape I was fascinated with how it looked and thought too many times “that looks more like a football shirt not a hat”.
I hope you enjoyed reading this long paragraph and looking at my design. I’ll end by saying that I’m glad I joined this competition because it showed me that my real friends are the one that brought me snacks while I was trying to finish this at lunch and that Textiles is not my subject.
192 Susan Corfield 50 UK
Doff your hat to Smith et al!
Proud print technician reveals…
Hats consistently… fit upon
Exciting geometry… shapes beyond
Composite kite complexion soars…
Irregular repetition solves…
Infinite possibility… wraps around
Mathematical beauty… shines on
Spectral tessellation tiles…
Collaborative imagination conceives…
Chiral symmetry… mirrors as
Perpetual complexity… stuns through
Sixty year einstein mission complete…
Doff your hat to Smith et al!
(And on it goes…)
Exciting geometry… shapes beyond
Infinite possibility… wraps around
Spectral tessellation tiles…
Sixty year einstein mission complete…
Irregular repetition solves…
Hats consistently… fit upon
191 Uttam Granhi 35 USA
In the demonstration below, geometric properties of the Einstein monotile were harnessed to create a mesmerizing physics-based effect. By stacking polarized Einstein monotiles in a plane and overlaying it with a rotating polarizer, a captivating flickering pattern was generated. This experiment can be further expanded to illustrate the chirality of sugars. Which not only highlights the connections between mathematics, physics, and chemistry but also serves as a testament to the inherent beauty that can be discovered at their intersection.
189 34 Luke Bryan USA
lease see full writeup at https://howtotrainyourrobot.com/einstein-hat-cylinder/
I found a way that you can have a periodic tiling of the Ein-stein tile on a cylinder! Please see the linked video in the post.
188 Luana De Souza 31 Brazil
The hats were sewn side by side, forming a central hexagon, this way it is possible to build tiles, balls or covers.